Pikkusemõõtjaid on erineva täpsusega

2.5. MÕÕTMISE TÄPSUS

Mõõteviga ja mõõtemääramatus

Mõõtmine on mõõdetava füüsikalise suuruse võrdlemine teise sama tüüpi suurusega, mis on mõõtühikuks kokku lepitud. Võrdlemise protseduur toimub aga alati olukorras, kus mõjuvad erinevad välised tingimused. Osa neist välismõjuritest võivad olla juhusliku iseloomuga ja paljud võivad olla meile ka teadmatud. Kõik see viib selleni, et mõõtmise tulemusel saadud väärtus ei pruugi suuruse tegeliku väärtusega täpselt kokku langeda. Tegelikult polegi absoluutselt täpne mõõtmine põhimõtteliselt võimalik. Kui midagi mõõdetakse, siis lisaks mõõtetulemuse saamisele on oluline hinnata ka mõõtmise täpsust. Kui aknaklaasijale antakse klaasi väljalõikamiseks mõõdud 1 m × 1,5 m ja ei täpsuatata, kuidas need saadud on, ei riski ta ise üle mõõtmata tööle asuda.

Tähistame mingi suuruse (näiteks pikkuse või massi) mõõtmisel saadud mõõtetulemuse tähega x. Kuna mõõtmine ei pruugi olla täpne, siis see mõõtetulemus võib mõõtesuuruse tõelisest väärtusest x0 erineda. Mõõtetulemuse ja suuruse tõelise väärtuse vahet nimetatakse mõõteveaks.
Suuruse x mõõteviga tähistatakse sageli sümboliga δx (loe väike delta x).

                δx = x - x0.

Mida väiksem mõõteviga, seda parem on mõõtmise täpsus.

Konkreetse mõõtmise korral on ainsaks informatsiooniks suuruse kohta saadud mõõtetulemus x. Kuna me mõõtevea väärtust ei tea, jääb mõõdetava suuruse tõeline väärtus alati teadmata. Mõõteviga on juhuslik suurus, mida pole võimalik kindlaks määrata. Iga järgmise mõõtmise tulemus võib eelmisest veidi erineda. Mõõtmisega kaasneb alati teatav teadmatus ehk määramatus. Suuruse tõeline väärtus jääb meile teadmatuks, kuid me saame anda tõenäosusliku hinnangu väärtuste vahemiku kohta, milles mõõdetava suuruse tõeline väärtus asub. Seda väärtuste vahemiku ulatust, kuhu suuruse tõeline väärtus sisse jääb, iseloomustab mõõtemääramatus. Mõõtemääramatust saab väljendada suurusega Δx (loe delta x), mille võrra mõõtetulemus x mõõdetud suuruse tõelisest väärtusest x0 rohkem erineda ei tohiks. Tõeline väärtus jääb vahemikku x - Δx kuni x + Δx. Matemaatiliselt väljendab seda võrratus:

            x - Δx < x0 < x + Δx.


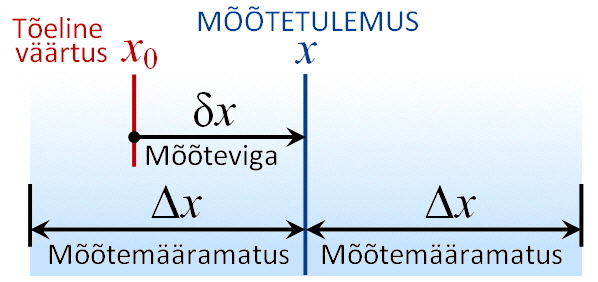
          Mõõtemääramatus näitab piirid, mille vahele mõõdetud suuruse tõeline väärtus jääb.

Mõõtemääramatus näitab, maksimaalselt kui suur võib mõõteviga olla. Vanemates mõõtmisalastes kirjutistes kasutataksegi mõõtemääramatuse asemel mõistet piirviga. Me võime mõõtevahendeid täiustades nende täpsust tõsta ja mõõtemääramatust vähendada, kuid seda päris ära kaotada pole võimalik. Mõõtemääramatuse hindamiseks on vaja teada selle allikaid.

Mõõtemääramatuse allikad

Mõõtemääramatuse hindamisel lähtutakse eeldusest, et mõõtetulemus on mõõdetava suuruse tõelise väärtuse parim hinnang. Mõõtemääramatuse leidmisel tuleb arvesse võtta kõik selle võimalikud komponendid.

Mõõtepraktikas on mõõtemääramatusel palju võimalikke allikaid. Toome siinkohal ära olulisemad faktorid, mis mõõtmistulemust mõjutavad:

Elektroonilised kaalud on erineva täpsusega                           Ajamõõtjad saavad tihti erinevaid tulemusi

Mõõtemääramatus ja mõõtetulemuse esitamine

Mõõtemääramatuse hindamiseks on erinevaid meetodeid. Mõnda neist tutvustatakse käesoleva konspekti järgmises peatükis. Kui määramatuse hinnangus on tehtud viga, ei saa me kunagi teada, kummale poole (suurendamise või vähendamise suunas) see tehtud on.

Igal juhul on selge, et mõõtemääramatuse alahindamine võib meid viia esitatud väärtuste liigsele usaldamisele, millel võivad olla väga ebameeldivad tagajärjed. Näiteks võib ebatäpse dopingutesti liigne usaldamineebaõiglaselt lõpetada süütu sportlase karjääri.

Ka määramatuse meelevaldne ülehindamine võib põhjustada soovimatuid tulemusi. See võib näiteks sundida mõõtevahendite kasutajaid hankima täpsemaid ja kallimaid mõõtevahendeid, kui neil tegelikult tarvis on. Tulemuseks on hindade tõus lõpptarbija ehk meie kõigi jaoks.Mõõtetulemus ilma mõõtemääramatuse hinnanguta on väärtusetu. Eespool oli toodud näide klaasilõikaja tööst. Aknaraami sobivat klaasi pole mõtet lõigata, kui selle mõõtude määramatus on 5 cm suurema või väiksema väärtuse suunas. Kui aga klaasissepp saab olla kindel, et mõõtemääramatus ei ületa 0,5 mm, asub ta aega viitmata tööle. Vastutusrikaste (sealhulgas teadustöös tehtavate) mõõtmiste tulemus tuleb esitada alati koos mõõtemääramatuse hinnanguga.

Mõõtetulemuse esitamisel tuleb alati anda parim hinnang mõõtesuuruse väärtusele ning parim lähend selle väärtuse määramatusele. Mõõtesuuruse parimaks hinnanguks on üldjuhul mõõtetulemus x ja selle määramatuse hinnangut väljendab suurim võimalik mõõteviga Δx. Koos saab neid esitada kujul mõõtesuurus = (x ± Δx) × mõõtühik.

Mõned näited:

< Tagasi     Sisukord      Edasi >


Metroloogia ehk mõõtmiste teaduse kohta saavad huvilised oma uudishimu rahuldada lugedes käesolevale konspektile lisaks järgmisi eestikeelseid raamatuid: