2.6. MÕÕTEMÄÄRAMATUSE HINDAMINE

Mõõtemääramatuse kaks tüüpi

Mõõtmine ei saa kunagi olla absoluutselt täpne. Sellega kaasneb alati teatav määramatus. Kui me ei tea, kui suur võib mõõtemääramatus olla, ei või me ka mõõtetulemust usaldada. Seepärast esitatakse usaldatav mõõtetulemus alati koos mõõtemääramatusega. Mõõtemääramatuse hindamiseks on erinevaid viise. Meetodi valik sõltub määramatuse tüübist.

Kui kordusmõõtmisi tehes saame kogu aeg veidi erinevaid tulemusi, mis varasematega täpselt kokku ei lange, on tegemist A-tüüpi määramatusega. A-tüüpi määramatus leitakse kordusmõõtmiste tulemustest statistiliste meetoditega. A-tüüpi määramatust saab mõõtmiste arvu suurendamisega vähendada.

Kui kordusmõõtmised annavad alati sama tulemuse, ei saa määramatust hinnata kordusmõõtmisi tehes. Sellisel juhul on tegemist B-tüüpi määramatusega. B-tüüpi määramatus saadakse muudest allikatest pärineva info põhjal,  näiteks kasutades mõõteriista tootja poolt antud mõõteriista täpsuse hinnangut.

Põhimõttelist erinevust nendel kahel määramatuse tüübil ei ole – mõlemad määramatused saadakse statistiliste uuringute põhjal. Vahe seisneb ainult määramatuse hindamise viisis.

A-tüüpi määramatuse hindamine

Kui mõõdame sama suurust mitu korda ja saame iga kord erineva tulemuse, tekib küsimus, millist neist siis kasutada tuleks? Milline neist kõige õigem on?

 Mõõdame näiteks, kui kõrgele põrkub 1 meetri kõrguselt lauale kukkuv pingpongipall. Pärast paari katset, mis annavad erinevaid tulemusi, saame aru, et siin ongi tegemist  A-tüüpi määramatusega. Sellisel juhul saab täpsust tõsta mõõtmiste arvu suurendamisega. Võtame mõõtmiste arvuks n = 100. Nimetatud mõõtmised on ka reaalselt läbi tehtud ja tulemusteks saadud järgmised sada arvu (mõõtühikuks on cm):

69, 75, 73, 72, 70, 72, 73, 72, 70, 75, 70, 74, 74, 75, 74, 76, 71, 70, 69, 77, 74, 69, 70, 75, 72, 75, 71, 72, 73, 69, 73, 71, 74, 73, 77, 72, 71, 73, 74, 74, 71, 72, 72, 72, 72, 74, 72, 73, 71, 71, 73, 74, 70, 70, 74, 73, 72, 71, 73, 76, 73, 71, 71, 68, 70, 73, 72, 71, 72, 72, 73, 72, 74, 70, 73, 71, 72, 72, 72, 74, 72, 73, 71, 73, 71, 75, 74, 75, 73, 71, 75, 73, 76, 74, 73, 72, 74, 72, 71, 73

Kui neid arve uurima hakata, võib täheldada, et samad mõõtetulemused korduvad aeg-ajalt, kuid mitte ühesuguse sagedusega. Kui 68 cm kõrgusele on pall põrganud vaid ühel ja 77 cm kõrgusele kahel korral, siis 72 cm kõrgusele tervelt 22 korda. Võib oletada, et tulemus, mis sagedamini kordub, on õigem. Matemaatilise statistika teooria kinnitab seda oletust ja ütleb, et juhusliku mõõteveaga suuruse mõõtmisel on ideaaljuhul tulemuse parimaks hinnanguks paljude mõõtmistulemuste aritmeetiline keskmine.

Aritmeetiline keskmine leitakse teatavasti kõikide tulemuste summa jagamisel tulemuste arvuga. Meie saja mõõtetulemuse aritmeetiline keskmine on 72,46 cm. Näeme, et enamus mõõtetulemustest tõepoolest omavadki sellele keskmisele lähedasi väärtusi.

Vaatame, kuidas meie mõõtmiste tulemused jaotunud on. Loeme kokku, kui sagedasti igat erinevat tulemust saadud on ning koostame vastava diagrammi. Sellist diagrammi nimetatakse mõõtetulemuste jaotumise histogrammiks.

Edasi lugedes klõpsa ka linkidele diagrammi kõrval asuvas tekstis.
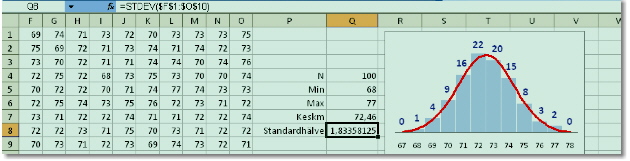
 Näeme, et tulemuste jaotumise histogramm on enam-vähem sümmeetriline.

Paigutades histogrammile tulemuste keskmist tähistava joone, näeme, et see asub täpselt keskel.

Kui mõõtmisi teha väga palju, saak-
sime tulpdiagrammi asemel sujuva joone, mis kirjeldab statistikas tuntud normaaljaotust.

Jaotuse laius iseloomustab mõõte-
määramatust. Normaaljaotuse laiust iseloomustab standardhälve σ, mille arvutamiseks mõõtetulemuste kaudu on olemas spetsiaalne protseduur. Meie katses tuleb σ = 1,83 cm.

Vaadates keskväärtusest kummalegi poole ühe standardhälbe võrra, jääb saadud vahemikku 68% tulemustest.
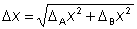Laiendades vahemikku kummalegi poole keskmist kahe standardhälbe võrra, jääb sellesse juba 95 % kõikidest mõõtetulemustest. Kolm standardhälvet kummalegi poole keskmist hõlmavad aga juba peaaegu kõik tulemused (tervenisti 99,7 %).

Eeltoodut kokku võttes tuleb juhusliku iseloomuga mõõtevigade ilmnemisel täpsuse tõstmiseks sooritada kordusmõõtmisi. Mõõtetulemuse parimaks hinnanguks võetakse nende aritmeetiline keskmine ning mõõtemääramatuseks sõltuvalt mõõtmise vastutusrikkusest 2...3 standardhälvet. Seejärel tuleb silmas pidada, et tulemust ei saa välja kirjutada täpsemalt kui mõõtemääramatus seda lubab.

Meie katse puhul võib seega 2σ korral tulemuse välja kirjutada kujul h = (72 ± 4) cm. Me võime üsna kindlalt väita, et igast sajast juhust põrkab pall 95 korral kõrgusele 68 - 76 cm.

Mõõtetulemuste aritmeetilist keskmist ja standardhälvet saab arvutada tabeltöötusprogrammide (näiteks MS Ecxel) ja paljude taskukalkulaatorite abil. Üks sobiv kalkulaator on tehtud kättesaadavaks ka käesoleva õppetüki lõpus.

B-tüüpi määramatuse ja kogumääramatuse hindamine

Nagu eespool öeldud, ei saa B-tüüpi mõõtemääramatust mõõtja ise kindlaks teha. Selle hindamine jääb mõõteriista tootja kohustuseks. Tootjad märgivad mõõtemääramatuse alase teabe kas otse mõõteriistale või selle passi. Kui aga selline info puudub, soovitatakse mõõtemääramatuseks võtta pool väikseimast skaalajaotisest.

Enamasti esinevad nii A- kui B-tüüpi määramatus korraga. Kogumääramatus leitakse kui ruutjuur nende ruutude summast. Tähistades suuruse x A-tüüpi määramatuse sümboliga ΔAx ja B-tüüpi määramatuse sümboliga ΔBx, on kogumääramatus
                                      .

< Tagasi     Sisukord      Edasi >

Kalkulaator aritmeetilise keskmise ja standardhälbe arvutamiseks

Sisesta mõõtetulemused arvuväljale, eraldades nad üksteisest komaga. Kümnendike eraldamiseks kasuta punkti. Näiteks: 25, 23.5, 32.4, 28, 26. Arvuvälja saab alt nurgast kinni võttes sobivasse suurusesse venitada.





Arvutustulemused:
Sisestatud andmete arv
Aritmeetiline keskmine
Standardhälve σ

Kalkulaator on võetud ja sobivaks kohendatud Internetilehelt  Easycalculation.com