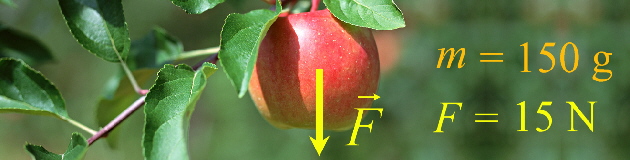

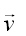 ja jõuvektori tähis
ja jõuvektori tähis 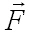
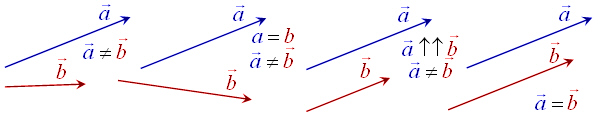
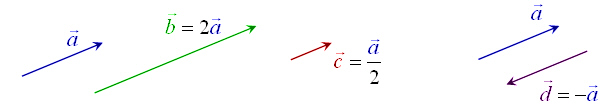
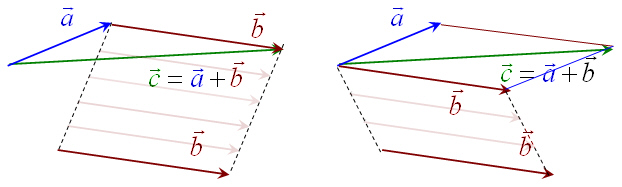
| Kolmnurga reegli järgi
liitmisel tuleb teine vektor nihutada nii, et selle algus ühtiks
esimese vektori lõpuga. Vektorite summaks on esimese vektoriri
algusest teise lõppu suunatud vektor. |
Rööpküliku
reegli järgi liitmisel tuleb teine vektor nihutada nii, et
mõlema alguspunktid langeksid kokku. Vektorite summaks on
liidetavatest vektoritest moodustuva rööpküliku
diagonaali suunaline vektor. |