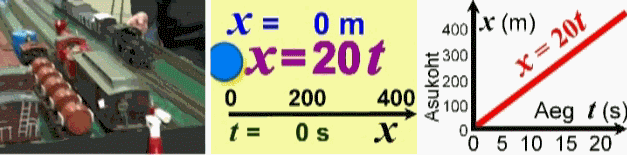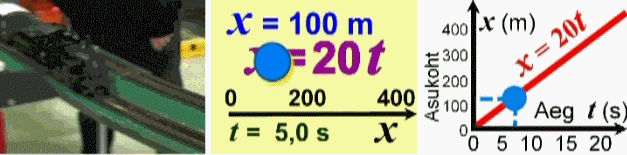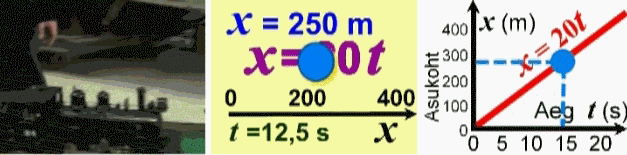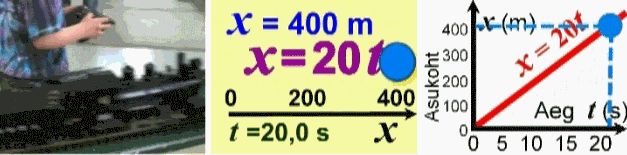Erinevate aegade ettekujutused aatomist ehk aatomimudelid
2.7. MUDELID FÜÜSIKAS
Mudeli mõiste ja liigid
Mudeliks (modulus —
ladina k mõõt, näidis) nimetatakse objekti
või nähtuse koopiat, mis asendab originaali selle
lihtsamaks mõistmiseks ning uurimiseks. Me teame, et
füüsikalises uurimistöös on tähtsal kohal
vaatlus. Vaatleja loob endale uuritavast objektist või
nähtusest kujutluse. Sellise füüsikalise
tunnetusprotsessi juures mängivad mudelid tähtsat rolli.
Mudeli saab luua mõnest objektist nagu vesinikuaatom,
raudteesild või galaktika. Modelleerida saab aga ka
füüsikalisi nähtusi nagu elektrivool, visatud oda lend
ja valguse murdumine vihmapiisas.
Kõikidele mudelitele on iseloomulik see, et nad ei kopeeri
originaali kunagi viimse detailini täpselt. Täpne kopeerimine
pole juba sellepärast võimalik, et me ei pruugigi
kõiki üksikasju näha ja pealegi puudub ideaalse
täpsuse järele ka vajadus. Mudelis kopeeritakse vaid
originaali kõige olulisemad tunnused ja omadused. Mudel on lihtsustus, kus
jäetakse arvestamata kõik mitteoluline. Looduslike
objektide ja nähtuste lihtsustatud mudeleid, mida kasutatakse
füüsikas maailma kirjeldamiseks, nimetatakse füüsikalisteks mudeliteks.
Mudelid, sealhulgas ka füüsikalised mudelid, saab liigitada ainelisteks mudeliteks ja abstraktseteks mudeliteks.
Ainelised mudelid
Mudeli saab meisterdada paberist, puidust, metallist, klaasist ja
plastmassist või mistahes muust sobivast ainest. Selliseid
niinimetatud ainelisi mudeleid saame palja silmaga vaadata ja soovi
korral ka käega katsuda. Ainelisi
mudeleid valmistatakse siis, kui uuritav objekt on vatlemiseks
liiga suur või väike. Näiteks aitab kellavedru
või elektrimootoriga käivitatav mehaaniline
Päikesesüsteemi vähendatud mudel paremini mõista
planeetide liikumist ning aastaaegade vaheldumist Maal. Geneetilise
informatsiooni talletamist DNA molekulis aitab aga mõista
miljoneid kordi suurendatud mudel.
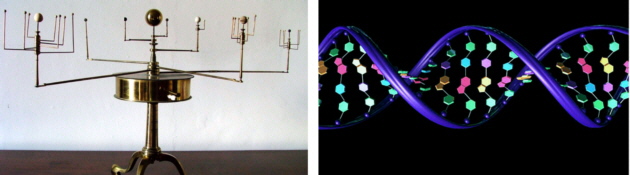
© www.arm.ac.uk Päikesesüsteemi vähendatud
mudel ©
www.turbosquid.com DNA molekuli suurendatud mudel
Aineliste mudelite alla saab liigitada ka kollektsioneerijate
poolt kogutavad automudelid, huviliste poolt ehitatavad mudellennukid
ning mänguasjade poes müüdav raudtee mudel. Selliste
mudelite eesmärk pole aga enamasti teadusega seotud. Need pole
füüsikalised mudelid.

Need on küll mudelid, kuid mitte
füüsikalised mudelid
Abstraktsed mudelid
Selleks, et ennustada, millal jõuab rong järgmisse jaama,
pole sugugi vaja rongi mudel puust välja nikerdada. Me
võime rongi lihtsalt ette kujutada. Seejuures pole üldse
tähtis, mitmest, kui kõrgest ning millist värvi
vagunitest see rong kokku pandud on. Lõppjaama jõudmise
aja ettearvamisel pole oluline, milline rong välja näeb, vaid
ainult see, kus ta asub erinevatel ajahetkedel. On vaja teada asukoha
sõltuvust ajast.
Sellise ülesande puhul piisab, kui kujutame tervet rongi ette vaid
punktina, millel mõõtmed puuduvad. Rongi
mõõtmed, kuju ja muud iseloomulikud suurused pole hetkel
olulised. Oluline on vaid see, kus see rongi tähistav punkt asub
ja kuidas selle asukoht aja jooksul muutub. Rongi liikumise
modelleerimiseks piisab, kui lihtsalt kujutame selle liikumist ette ja
esitame matemaatilise valemi, mis lubab rongi asukoha mistahes
ajahetkel välja arvutada. Rongisõidu
nähtust on võimalik
kirjeldada matemaatiliste avaldistega. Juhul, kui
füüsikalist objekti või nähtust uuritakse ja
kirjeldatakse mitte ainelise mudeli, vaid mõtteliste
ettekujutuste ning neid väljendavate matemaatiliste avaldiste
abil, on tegemist abstraktse mudeliga.
Sõna
abstraktne
tuleneb
ladinakeelsest sõnast abstractus,
mis
tähendab
eraldiseisvat ehk mõttelist. Abstraktne mudel on objekti
või nähtuse mõtteline
visioon.
Rongi liikumise visiooni ehk mõttelist kujutluspilti saab
abstraktselt modelleerida matemaatilise
avaldisega, mis lubab liikumise iseloomu teades
välja arvutada rongi kaugust lähtejaamast mistahes
võimalikul ajahetkel. Kui rongi kaugust lähtejaamast
(meetrites) tähistada tähega x ja aega, mis liikumahakkamisest
möödunud on, tähega t
(sekundites), väljendab selle rongi liikumist näiteks
avaldis x = 20•t. See avaldis kujutabki
endast rongi liikumist kirjeldavat matemaatiline mudelit. Meile piisab,
kui kujutame rongisõitu vaid ette ning saame valemi
abil välja arvutada, et aja 30
minuti
ehk
t = 1800 sekundiga
jõuab rong kaugusele x
= 20×1800 = 36 000 m ehk 36 km. Äsja kasutatud
matemaatilisele avaldisele tuginevat rongi liikumise kirjeldust
nimetatakse liikumise analüütiliseks
mudeliks. Rongi asukoha sõltuvust ajast saab peale
matemaatilise valemi väljendada ka graafiku abil. Sel puhul on
tegemist nähtuvuse graafilise
mudeliga.
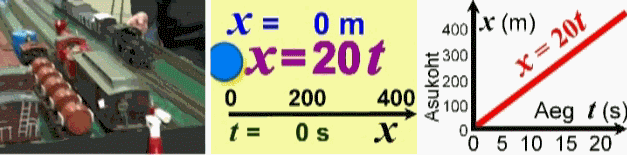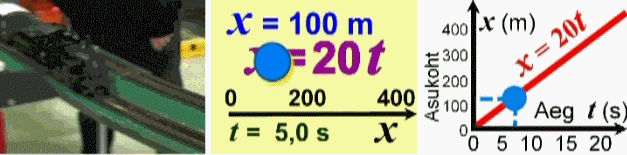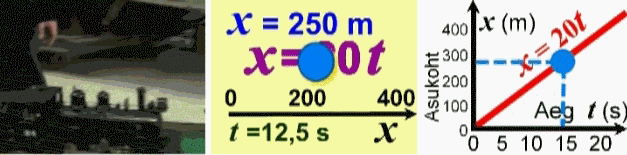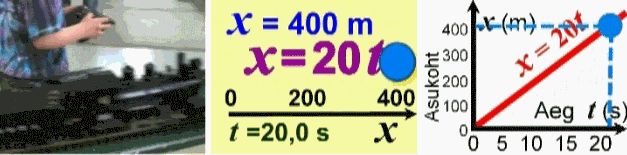
Aineline
mudel
Abstraktne
analüütiline
mudel
Abstraktne
graafiline mudel
< Tagasi
Sisukord
Edasi >